在高中数学中，求解最小值是一种常见的问题。无论是在代数、几何还是函数的应用中，寻找最小值都是解题过程中的重要一环。本文将介绍一些高中数学中常用的方法和技巧，帮助读者更好地应对最小值问题。

一、最小值的定义与特性

1.1最小值的定义及其在数学中的应用

-最小值定义：某个中数值最小的元素，也称为最小值。

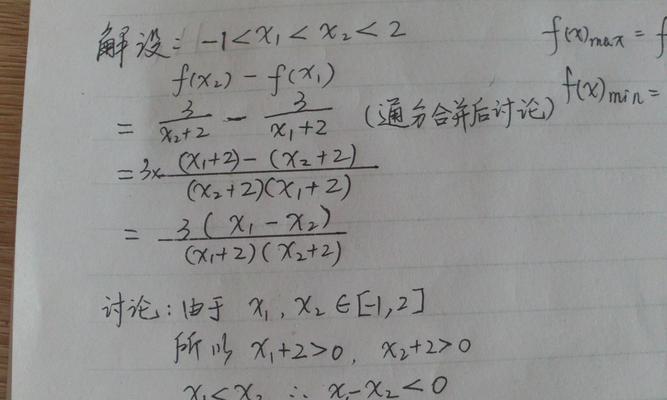
-最小值在数学中的应用：在函数图像中，最小值对应着函数图像的最低点；在求解优化问题时，我们常常需要寻找某个变量或参数的最小值。

1.2最小值的特性及相关定理

-最小值存在性定理：如果一个函数在闭区间上连续，则它在该区间上一定有最大值和最小值。

-极值点和驻点：驻点是函数导数为零的点，而极值点是函数图像上的局部极大值或极小值点。

二、代数方法求最小值

2.1平方差公式的应用

-平方差公式：a2-2ab+b2=(a-b)2，常用于将二次多项式转化为平方差的形式，便于求解最小值。

2.2配方法的应用

-配方法：将一个二次多项式进行配方，使其转化为完全平方或差的平方，从而找到最小值。

2.3求导法求最小值

-求导法：对函数进行求导，并将导函数等于零的点作为候选最小值点，然后进行验证。

三、几何方法求最小值

3.1几何平均与算术平均的关系

-几何平均与算术平均：几何平均数是指若干个数连乘后开方得到的结果；算术平均数是指若干个数之和除以个数的结果。

3.2最短距离与最小值问题

-最短距离问题：在几何图形中，寻找两点之间的最短距离，可以通过求解最小值问题来解决。

四、函数方法求最小值

4.1利用函数性质求最小值

-函数性质：函数在定义域上是否单调、是否有上下界等特性，可以帮助我们判断最小值的位置。

4.2运用函数图像求最小值

-函数图像的凸性：函数图像的凹凸性可以帮助我们判断最小值点的位置。

五、优化问题与最小值

5.1优化问题的基本思路与方法

-优化问题：在一定条件下，寻找某个目标的最大值或最小值，是一类常见的问题类型。

5.2利用约束条件求最小值

-约束条件：在优化问题中，往往会有一些限制条件，通过加入约束条件来求解最小值。

六、

通过本文的介绍，我们了解了在高中数学中求解最小值的常用方法和技巧。无论是代数、几何还是函数，我们可以根据问题特点选择合适的方法来求解最小值。掌握这些技巧，可以更好地应对高中数学中的最小值问题。